Solitary waves
What are solitary waves?
Solitary waves are a special class of water waves. For the purposes of this project, they are best defined by a single elevation in the water surface. A soliton will typically span the entire width of a canal. Such a wave is most likely to be seen on its own, upstream of any boat because solitons move faster than the boat that created them and can travel a very long distance without changing shape.
How are solitary waves generated?
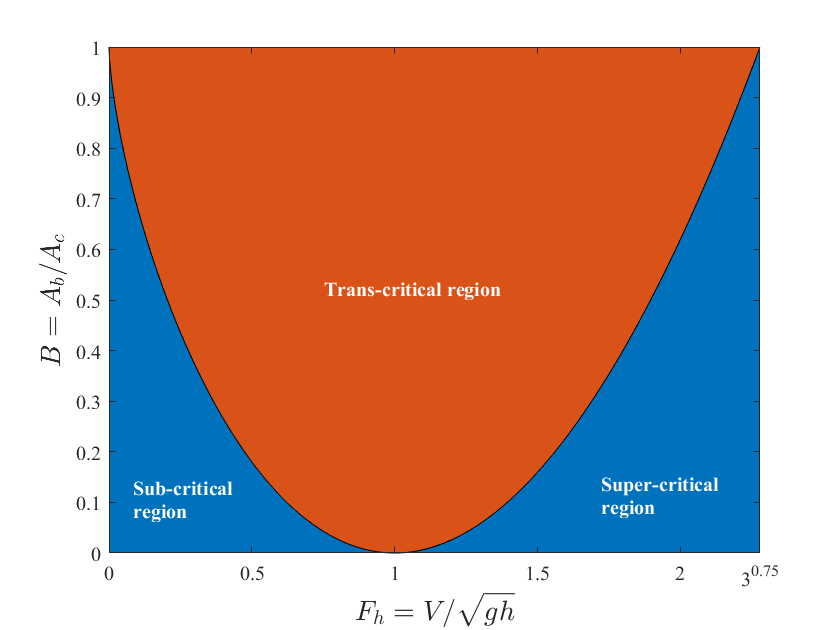
Solitary waves are generated when a vessel enters the so-called trans-critical region in terms of blockage and speed.
We can express the blockage as $B=A_b/A_c$ where $A_c$ is the canal cross-sectional area and $A_b$ is the boat midship cross sectional area. We also make the speed ($V$) dimensionless by dividing it by the speed of the wave $c=\surd(gh)$, with $g=9.81m/s^2$ and $h$ being the water depth. We call that ratio the depth Froude number $F_h=V/\surd(gh)$ which is analogous to the Mach number in aerodynamics. The figure below shows the three possible flow regimes:
- Subcritical: the depth Froude number is below $1$ and steady flow is possible.
- Trans-critical: the depth Froude number can be $F_h>1$ or $F_h<1$, but no steady flow is possible
- Supercritical: the depth Froude number is higher than 1 and steady flow is possible.
The image below was constructed using: $$B_{crit}=1-sin(3arcsin(F_h^{2/3}/2))$$
What does solitary wave generation look like?
It is convenient to use wavecuts to study how the water surface deforms due to the presence of a boat. Below is an example illustrating what a wave cut is and how we interpret this data.
Credit: Mr Patrick Reid A snapshop of the animation above in 3D:
Credit: Mr Patrick Reid Next steps
I will add a calculator that gives the critical blockage for a given depth Froude number